Discounted Cash Flow Valuation Part 1

Created by David Moore, PhD

Reference Material: Wall Street Prep DCF Modeling Chapter 3 and 5

Key Concepts

  1. Terminal Value
    • Perpetuity Growth Rate
    • Exit Multiple
  2. Cost of Capital
    • Estimating Weights
    • Beta and the Cost of Equity
    • Cost of debt
  3. Enterprise Value

DCF Overview



  • Free Cash flows (forecast period)
  • Terminal Value
  • Discount rate

Infinite Horizon Problem

  • Assume a fixed length forecast window
  • Followed by terminal window of infinite length

Terminal Value

Terminal 1: Perpetuity Growth Rate

  • Growing Perpetuity
  • Need a discount rate (r)
  • Need a growth rate (g)

Growing Perpetuity

A growing perpetuity is a growing stream of cash flows that lasts forever

$PV=\frac{C}{r-g}$

Important: Growth rate (g) must be less that interest rate r. If g>r the formula will not work!

Example_1

Given an interest rate of 7 percent per year, what is the value at date t = 8 of a perpetual stream of 500 annual payments that begins at date t = 17 and grows at 5% thereafter? What if the growth rate was 10%?

Example_1 Solution

Given an interest rate of 7 percent per year, what is the value at date t = 8 of a perpetual stream of 500 annual payments that begins at date t = 17 and grows at 5% thereafter?

$PV_{t=16}=\frac{500}{.07-.05}=25000$

$PV_{t=8}=\frac{25000}{(1+.07)^{16-8}}=14550.23$

What if the growth rate was 10%?
r<g ; cannot solve

Getting the Rates

  1. r: Use the WACC (more on this later)
  2. g: A reasonable assumption must be less than the growth rate of overall economy
    • Good Assumption: Nominal risk free rate = real Rf rate + expected inflation
    • Typical range for g is 2-5%
    • 2009-2015 Risk free:2.57% GDP: 3.14%


FRED Website OECD

Terminal 2: Exit Multiple

  • Apply valuation multiple to operating metric
  • Typical to use comparables Damodaran Website


$Terminal Value= Multiple*Operating Metric$

Example (typical): EBITDA ratio x EBITDA in terminal year.

PV of Terminal Value



Need to discount the terminal value using the appropriate discount rate.

  • Can be a different discount rate than rate used for terminal window

Issues with Terminal Value Methods

  • Perpetuity Growth: Technically sound but requires assumption of when stable growth begins AND stable growth rate.
  • Multiples: Makes the valuation a relative (rather than intrinsic) valuation.

Revisit Example 1

SIC

Revisit Example 2

SIC

Cost of Capital

First Principle of Valuation

Who do unlevered cash flows belong to?

Discounting Consistency Principle: Never mix and match cash flows and discount rate

Appropriate Discount Rate?

  • Free cash flows to the firm discount at cost of capital to the FIRM
  • WACC is used as estimate of cost of capital if valuing the entire firm
  • Discussed later: Levered cash flows (to equity) use Cost of Equity

What is a Discount rate?

Should reflect the riskiness and type of cashflow being discounted
  • Incorporate all risk that affect the asset (business)
  • Reflect the risk perceived by the marginal investor
  • Opportunity cost of taking on risk of investing in the company
  • Required return
    • Return to investor is the same as cost to the company

Cost of Capital (WACC)

  • The firm's assets are financed through debt and equity (RHS of Balance sheet)
  • We can use the individual costs of capital for debt and equity to get our "average" cost of capital for the firm
  • This "average" is the required return on the firm's assets, based on the market's perception of the risk of those assets
  • The weights are determined by how much of each type of financing is used

Cost of Equity

Rate of Return (opportunity cost) demanded by equity investors.

  • Who is the equity investor?
  • What risks do they face?
  • What is their opportunity cost?

Cost of Debt

Rate of Return (opportunity cost) demanded by debt investors.

  • Cost of debt is not the coupon rate
  • Interested in yield if the firm issued more debt.
    • Rate at which you could borrow currently
  • Only concerns long-term debt. (Why?)
  • Is all debt observable?

Capital Structure Weights

Should we use book or market values?
  • Notation
    • E = market value of equity
    • D = market value of debt
    • V = market value of the firm = D + E
  • Weights
    • $w_E = \frac{E}{V} =$ percent financed with equity
    • $w_D=\frac{D}{V}=$ percent financed with debt

Taxes

  • We are concerned with after-tax cash flows, so we also need to consider the effect of taxes on the various costs of capital
  • Interest expense reduces our tax liability
    • This reduction in taxes reduces our cost of debt
  • Dividends are not tax deductible, so there is no tax impact on the cost of equity
  • We use the marginal tax rate

WACC



$WACC=w_ER_E+w_DR_D(1-T_C)$

$w_E$=Weight of Equity
$R_E$=Cost of Equity
$w_D$=Weight of Debt
$R_D$=Cost of Debt
$T_C$=Marginal Corporate Tax rate

Simple Example


The estimated market value of a firm's debt (book value) is 4 million and the market cap is 6 million. The cost of equity is 10% and the cost of debt is 6%. The marginal tax rate is 21%. What is the cost of capital for this firm i.e., What is the WACC?

Answer:7.896%

Estimating Weights

  • Equity: Market value of Equity
    • Shares outstanding X Share price


  • Debt: Market value of debt
    • Unobservable...

Estimating Market Value of Debt

  • Standard to use Book value of debt
  • Only concerned with Long-term Debt!
  • Don't forget current portion of LTD
  • Also include Notes payable or Lease obligations (any interest bearing long term debt)
  • Some Modelers include cash as negative debt (we will not)

Example

What are the market weights for a firm with a share price of $18.5 and 30.5 million shares outstanding. The firm has long-term debt of $385 million and shows $35 million under current portion of long-term debt?

Answer: Weight of Equity = 57.33% and Weight of Debt = 42.67%

Estimating Cost of Debt

  • Two Methods
    1. Yield
    2. Default Spreads

Yield

  • Use yield on long-term (10-30 year) straight bonds
  • Find yields here
  • Major issue is most companies do not offer long term straight bonds that are liquid and widely traded

Default Spreads

  • Use the firm rating to estimate the default spread.
  • Find default spreads here
  • Add default spread to risk free rate
    • 10-year rate is most liquid and allows for calculation of default spreads
  • Use synthetic rating if firm has bonds with different ratings
  • No bond rating? Use interest coverage ratio

Cost of Equity

What makes up a risk adjusted cost of equity?

  1. Risk free rate
  2. Relative risk of company
  3. Equity Risk Premium

Market Risk Models

  • Capital Asset Pricing Model (CAPM)
  • Multi-factor Models (won't be using)

The Capital Asset Pricing Model (CAPM)

The capital asset pricing model defines the relationship between risk and return

$E(R_i)=R_f+\beta_i(E(R_M)-R_f)$

  • If we know an asset's systematic risk, we can use the CAPM to determine its expected return
  • This is true whether we are talking about financial assets or physical assets

Market Equilibrium

In equilibrium, all assets and portfolios must have the same reward-to-risk ratio, and they all must equal the reward-to-risk ratio for the market

$\frac{E(R_A)-R_f}{\beta_A}=\frac{E(R_M)-R_f}{\beta_M}$

Security Market Line

  • The security market line (SML) is the representation of market equilibrium
  • The slope of the SML is the reward-to-risk ratio: $\frac{E(R_M)-R_f}{\beta_M}$
  • But since the beta for the market is always equal to one, the slope can be rewritten
  • Slope $=E(R_M) – R_f =$ market risk premium

Factors Affecting Expected Return

  1. Pure time value of money: measured by the risk-free rate
  2. Reward for bearing systematic risk: measured by the market risk premium
  3. Amount of systematic risk: measured by beta

Simple Example

What is the expected return for a company with a beta of 1.5 if the risk free rate is 3% and the market risk premium is 7%?


Answer: 13.5

Risk Free Rate ($R_f$)

A risk free investment has no variance around the expected return. i.e., return is guaranteed

Investment must have:
  • No default risk
  • No reinvestment risk
    • Time horizon and zero-coupon


  • We will proxy with 10-year Treasury Bond
  • Note: Currency matters (if non-USD)

Should you Normalize risk free rate?

NO!
  • Risk free is alternative investment to stock

Beta

Measure of a stocks volatility (systematic risk) relative to the market

$\beta_{Equity}=\frac{Cov(R_i,R_M)}{Var(R_M)}=\frac{\sigma_{i,M}}{\sigma_M^2}$

, which is equal to the slope from regressing firm returns on market returns

Issues with (Regression) Beta

  1. High standard error (Remember Statistics!)
  2. It is backward looking
    • It reflects the firm's business mix over the period of the regression, not the current mix
    • It reflects the firm's average financial leverage over the period rather than the current leverage.
    • Requires data

Determinants of Beta

  • Business risk
    • Asset/Industry Beta
    • Nature of product/service offered and operational leverage
  • Financial risk
    • Leverage

Beta and Leverage

$\beta_{Equity}=(1+(\frac{D}{E}*(1-T_C))\beta_{Asset}$

Note: Assumes riskless debt i.e., debt has a beta of zero.

Ideal Beta (for valuation)

  1. Start with beta of the business that firm is in
  2. Adjust business beta for operating leverage
  3. Use the financial leverage of the firm to estimate the equity beta for the firm

Bottom Up Beta

  • Unlever comparable industry peer betas (i.e., compute asset betas)
  • Average them, to get an estimate of the industry (asset) beta
  • Lever the average industry beta to the firm's (optimal) capital structure

Why Bottom Up?

  • Lower Standard error
  • Adjusted to reflect changes in business and financial risk
  • Does not require historical stock prices

Conglomerates

  • Can calculate an asset beta for each business sector
  • Weight each asset beta by market value
    • Issue is market value unknown
    • Ideally you would estimate
    • Alternatives are to use revenue or operating income

Market (Equity) Risk Premium

In theory, the market risk premium is the forward-looking expected return on the market in excess of the forward-looking risk-free rate
  • Analysts(lack of) consensus: 1-10%
  • 6.5% – 8.5% most common
  • 1926 – 2005 period, large U.S. stocks averaged 8.5% higher returns than T-bills
  • Damodaran to the rescue

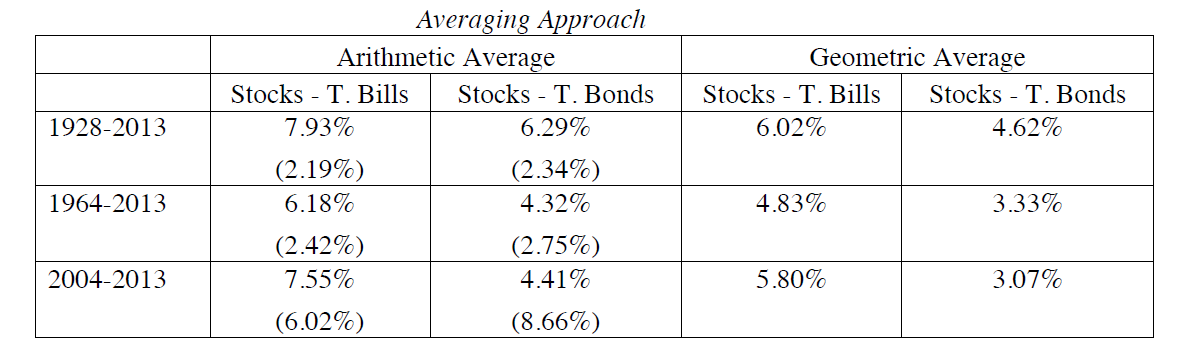
Historical ERP

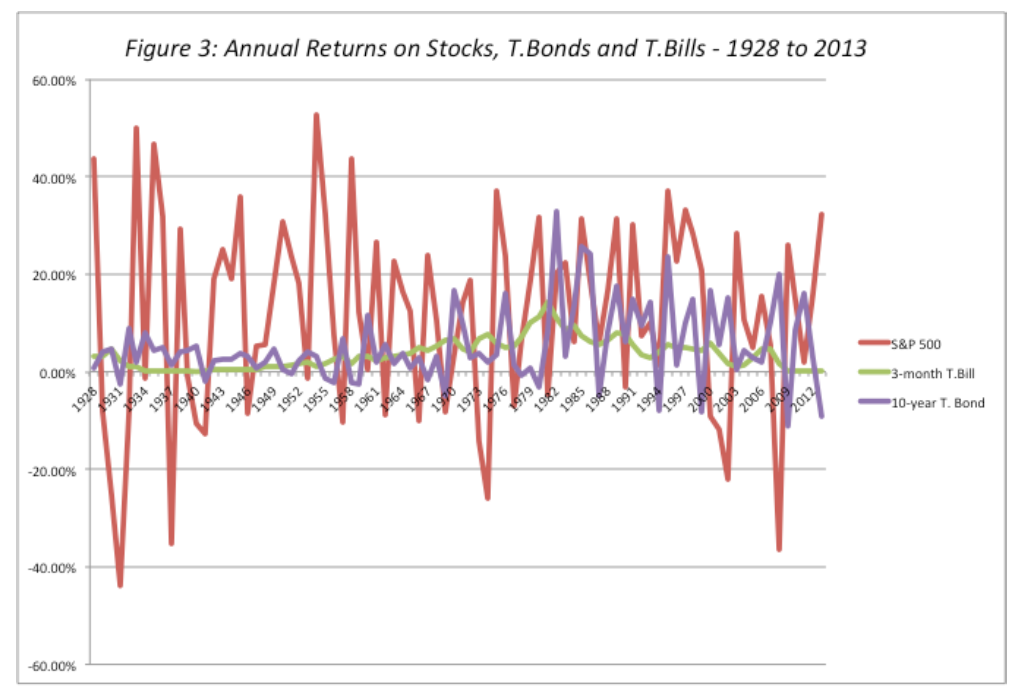
error

Averaging

error

Let's practice!

  • Calculate Stryker(SYK) Beta (using historical prices)
  • Using CAPM What is Stryker's Cost of equity?
  • Using Cardinal Health (CAH), Medtronic (MDT), Abbott Laboratories (ABT) and Boston Scientific (BSX) calculate the bottom up beta. Assume a tax rate of 21%.

Forecast vs Terminal Window

  • Can use different rates
  • Standard for terminal rate to be lower
  • Lower because slowed growth and (presumably) lower risk
  • Possible assumption: Industry average beta (lower)

Enterprise Value

  • We've valued FCFF at the cost of capital to the firm
  • Enterprise value is FIRM value
  • Equity Value=Enterprise Value - Net Debt
    • Net Debt= Debt-Cash
  • Also need to remove preferred stock and non-controlling interest

Revisit Gentex

SIC

Revisit Alaska Airlines

SIC

Next time

Discounted Cash Flows Part 2