Risk, Return, and Cost of Capital

Created by David Moore, PhD

Reference Material: Chapter 12, 13 and 14 of Textbook

Topics

  1. First Lesson: Average Returns
  2. Second Lesson: Variability of Returns
  3. Arithmetic vs Geometric Returns
  4. Capital Market Efficiency
  5. Expected Returns and Variances
  6. Portfolios
  7. Diversification
    • Total, systematic, unsystematic risk
    • Beta
    • Reward-to-risk Ratio
    • Security Market Line and CAPM
  8. Cost of Capital

Overview: Risk, Return and Financial Markets

  • Lessons from capital market history
    • There is a reward for bearing risk
    • The greater the potential reward, the greater the risk
    • This is called the risk-return trade-off


How should we measure risk and return?

First Lesson: Average Return

Historical Record

Uber

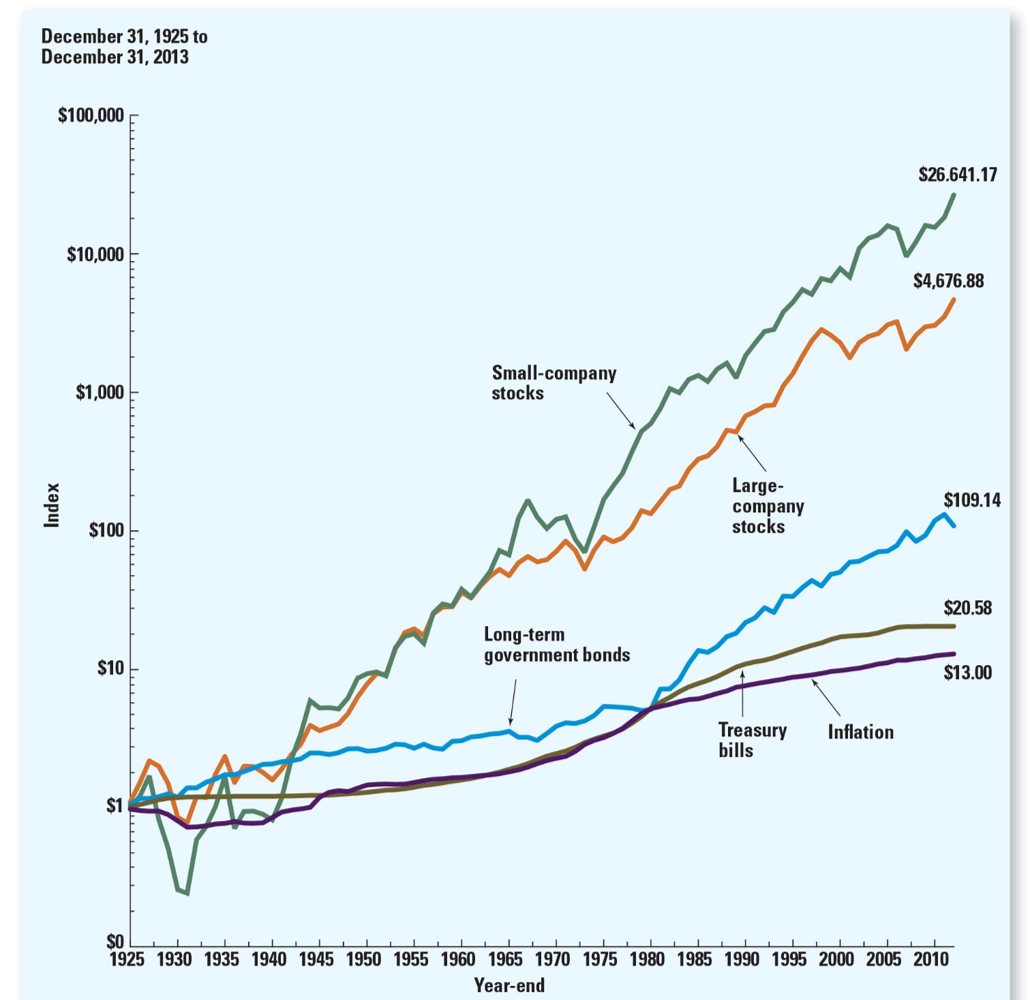
Ranking Returns

  1. Small cap stocks
  2. Large cap stocks
  3. Long-term government bonds
  4. Treasury Bills
  5. Inflation


Why wouldn't you just buy small cap stocks?
RISK!!!!

Calculating Returns

  1. Total Dollar Return

    • $Return = Dividends + Capital Gains

  2. Total Percent Return

    • %Return = $\frac{\$Return}{\$Invested}$

Example: Returns

You just invested in "You call that a Donut! Inc" for $\$$25, after one-year the price is $\$$35. Each share paid out a $\$$2 dividend. What was your total return?

Dollar Return Percent Return
Dividend 2 $\frac{2}{25}=8\%$
Capital Gains 35-25=10 $\frac{35-25}{25}=40\%$
Total Return 2+10=12 $\frac{10+2}{25}=48\%$

Percent Returns: Formulas

Dividend Yield
$DY=\frac{D_{t+1}}{P_t}$

Capital Gains Yield
$CGY=\frac{P_{t-1}-P_t}{P_t}$

$\%Return=\frac{D_{t+1}+P_{t+1}-P_t}{P_t}$

Historical Average Returns


$HistoricalAverageReturn=\frac{\sum\limits_{i=1}^TReturn_i}{T}$

Large cap stocks average return from 1926 to 2010: 12.1%

Your best guess about the size of the return for a year selected at random is 12.1%.

Historical Average Returns: 1926-2010

Uber

Practice: Average

Returns: -6, 8, 12, -15, 6

Average = 1

Returns: -1, 2, -1, 1, 4

Average = 1

Risk Premium

The excess return required from an investment in a risky asset over that required from a risk free investment.
Uber
U.S. Treasury bill is considered risk-free return

Historical Average Risk Premium

Uber

First Lesson Takeaways

Risky assets, on average, earn a risk premium

Large company stocks have a historical average risk premium of 8.6%

What determines size of risk premium?

Second Lesson: Return Variability

Measuring Return Variability

  • Variance or $\sigma^2$
    • Common measure of return dispersion
  • Standard deviation or $\sigma$
    • Sometimes called volatility
    • Same "units" as the average

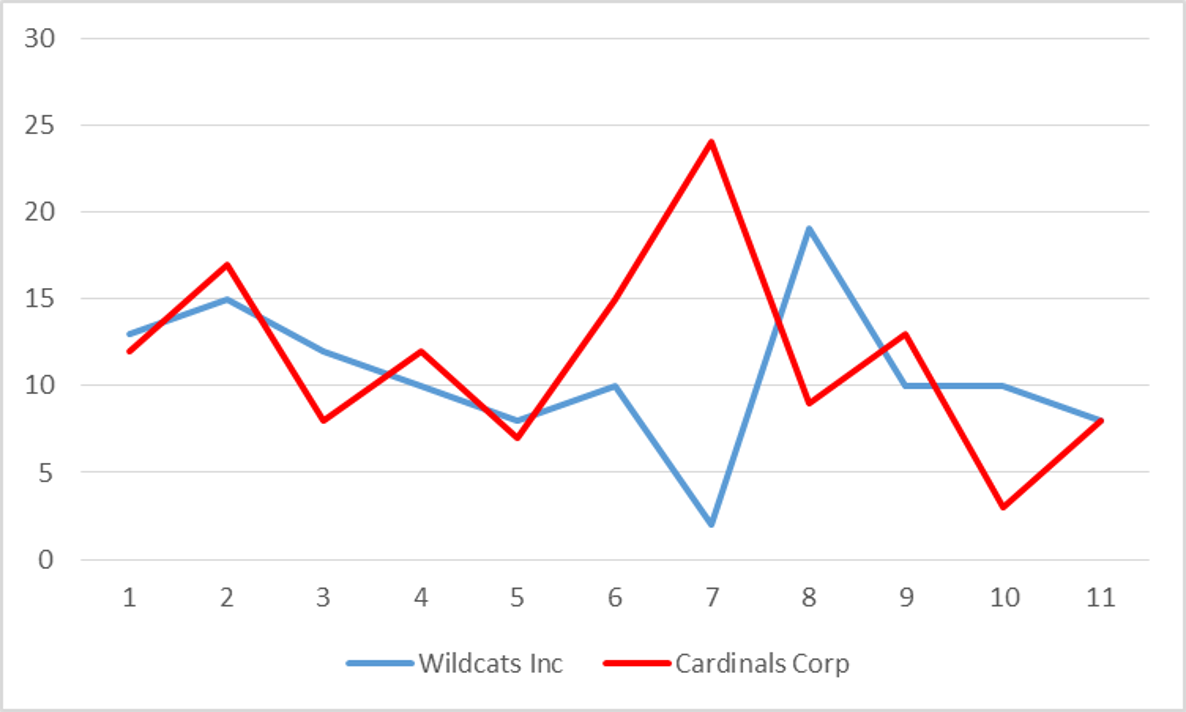
Example

Two companies have the following returns:
Wildcat Inc: 13,15,12,10,8,10,2,19,10,10,8
Cardinals Corp: 12,17,8,12,7,15,24,9,13,3,8

Wildcats Inc. Cardinals Corp.
Average 10.6 11.6
Standard Deviation 4.3 5.7

Graphical Representation

Uber

Steph vs LeBron (Points in 2016 Playoffs)

Steph Curry (9 games leading into finals):40,29,26,28,24,19,31,31,36.
LeBron James (9 games leading into finals):27,24,21,24,23,24,29,23,33.

Steph LeBron
Average 29.33 25.33
Standard Deviation 6.25 3.71

Return Variability

  • Return Variance:


$VAR(R)=\sigma^2=\frac{\sum\limits_{i=1}^T(R_i-\bar{R})^2}{T-1}$

  • Standard deviation:


$STD(R)=\sigma=\sqrt{VAR(R)}$

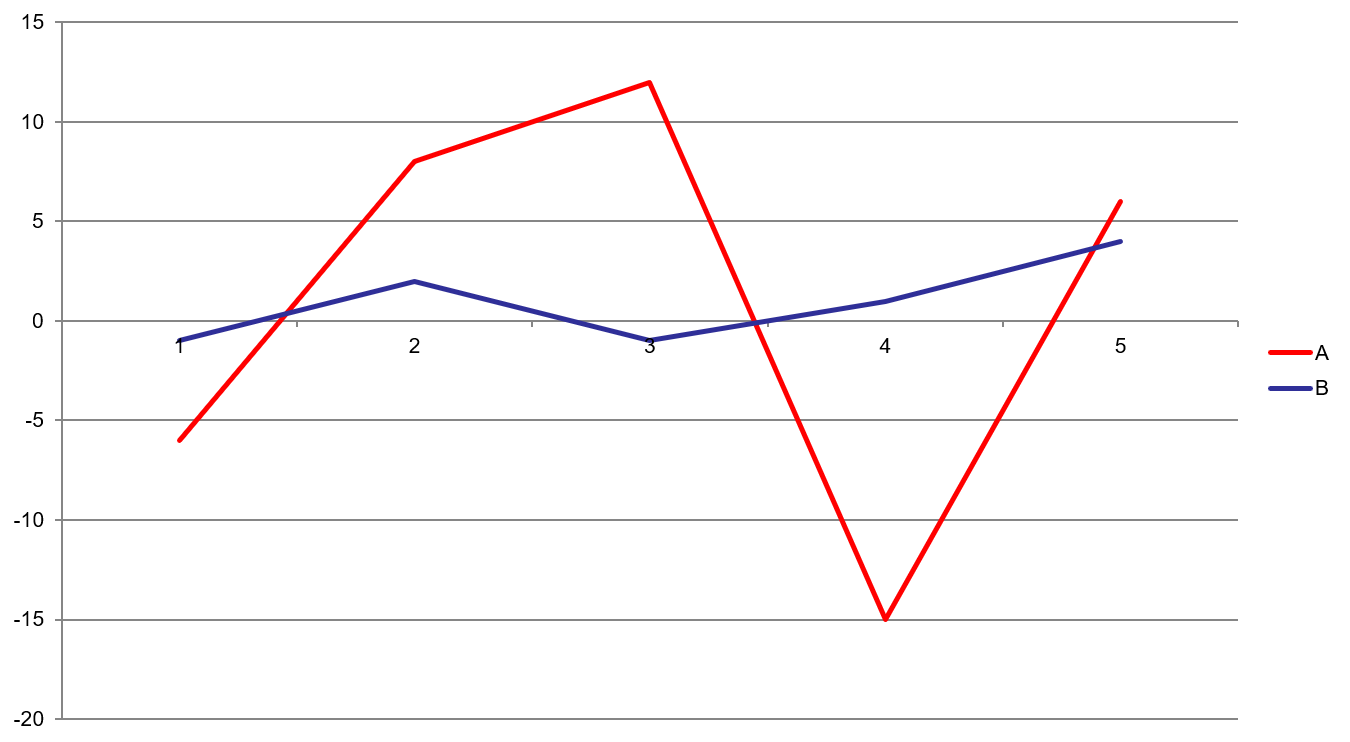
Practice: Standard Deviation

Returns(A): -6, 8, 12, -15, 6

Average = 1
Standard deviation = 11.18

Returns(B): -1, 2, -1, 1, 4

Average = 1
Standard deviation = 2.12

Graphing Returns

Uber

Example

Year Return (%) Average Return (%) Difference Squared Difference
1926 11.14 11.48 -.034 0.0012
1927 37.13 11.48 25.65 657.82
1928 43.31 11.48 31.83 1013.02
1929 -8.91 11.48 -20.39 415.83
1930 -25.26 11.48 -36.74 1349.97
Variance 859.19
Standard Deviation 29.31

Normal Distribution

A symmetric bell-shaped frequency distribution that is completely defined by its mean and standard deviation.
Uber

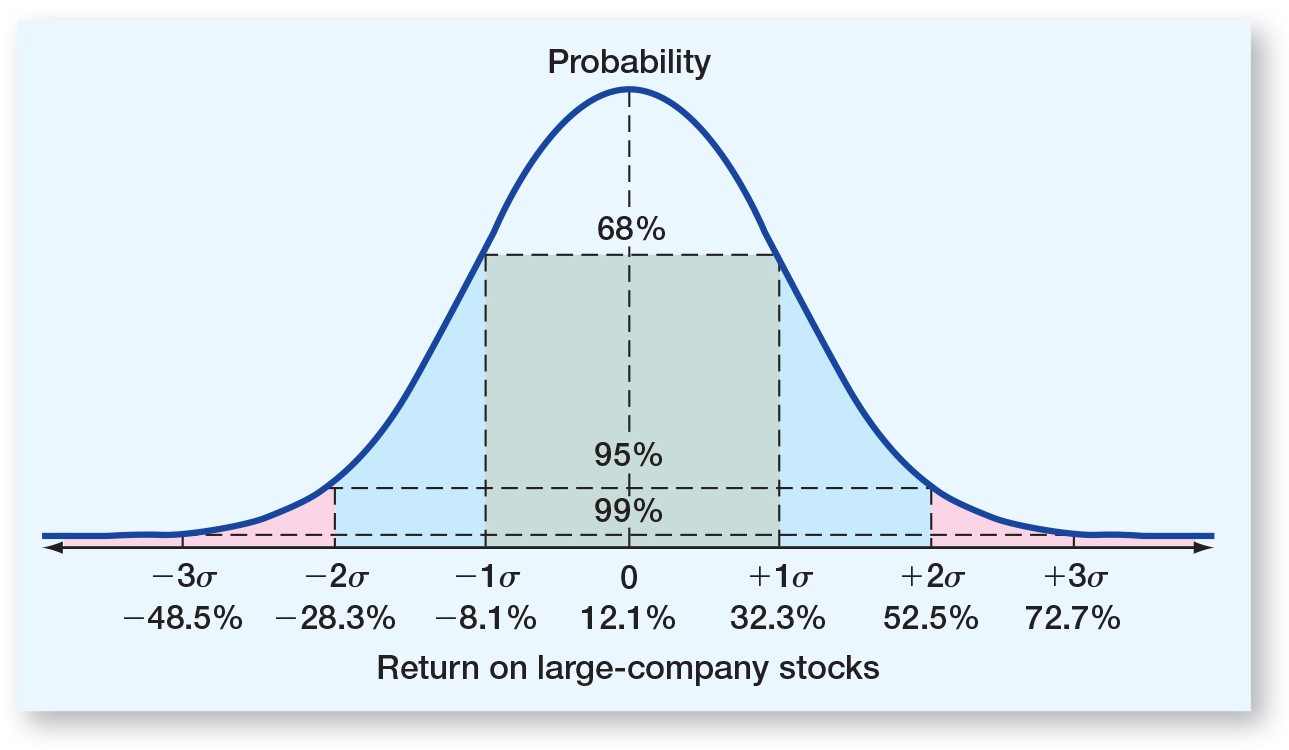
Arithmetic vs. Geometric Mean

Think about returns...

If you invest in a hedge fund that loses 20% the first year, but makes 20% the second year, are you back to even?

  • NO!!!!!
  • Start with $\$$100
  • After year 1: you have $\$$80
  • After year 2, you have $96

Another example

Suppose you invest $\$$100 and it falls 50% in year one but gain 100% in year 2.

  • Year 0:100
  • Year 1:100*(1-0.50)=50
  • Year 2:50*(1+1)=100

Arithmetic vs. Geometric Mean

  • Arithmetic average:
    • Return earned in an average period over multiple periods
    • Answers the question: "What was your return in an average year over a particular period?"
  • Geometric average
    • Average compound return per period over multiple periods
    • Answers the question: "What was your average compound return per year over a particular period?"


Geometric average < Arithmetic average unless all the returns are equal

Geometric Average: Formula


$GAR=[(1+R_1)*(1+R_2)*...*(1+R_T)]^{\frac{1}{T}}-1$

Where:
$R_i$= return in each period
$T$ = number of periods

Geometric Average: Formula


$GAR=[\prod\limits_{i=1}^T(1+R_i)]^{\frac{1}{T}}-1$

Where:
$\prod$= Symbol for product (multiply)
$R_i$= return in each period
$T$ = number of periods in sample

Revisit Examples

If you invest in a hedge fund that loses 20% the first year, but makes 20% the second year.
Average Return: 0%
Geometric return: -2.02%

Suppose you invest $\$$100 and it falls 50% in year one but gain 100% in year 2.
Average Return: 25%
Geometric Return: 0%

Example

Year Return (%) (1+R) Compounded
1926 11.14 1.114 1.114
1927 37.13 1.3713 1.5241
1928 43.31 1.4331 2.1841
1929 -8.91 0.9109 1.9895
1930 -25.26 0.7474 1.4870
$(1.4870)^\frac{1}{5}$ 1.0826
Geometric return 8.26%

Capital Market Efficiency

Capital Market Efficiency

A market in which security prices reflect available information
Uber
If true, cannot earn abnormal or excess returns.

Efficient Market Hypothesis

The hypothesis that actual capital markets are efficient.

  • Idea is competition among investors drives information into prices and thus the market becomes more and more efficient.
  • Stocks are all priced correctly

Finance version of "Dad Joke"

A student and a finance professor are walking down the hall when they both see a $\$$20 bill on the ground. The student bends down to pick it up.

The professor shakes their head slowly with a look of disappointment. And says…

"Don't bother, If it were really there, someone else would have picked it up already"

Forms of Market Efficiency

  1. Strong form: all information of every kind is reflected in the stock prices. Including public and private.
  2. Semi-strong form: all public information is reflected in stock prices.
  3. Weak form: Prices reflect all past trading information such as prices and volume.

Summary

  • No simple way to "beat" the market
  • Identifying mispriced stocks is very difficult (borderline impossible)
  • Prices do respond rapidly to information
  • Very difficult to predict future stock prices

Expected Returns and Variances

Weighted Average Reminder

Your grade is weighted 30% for the midterm 50% for the final. Homework is worth 10% and quizzes another 10%. You did perfect on the homework and quizzes. The midterm you received a 81 and the final was an 92. What is your final grade?

Answer: 90.3

Expected Returns

  • Expected returns are based on the probabilities of possible outcomes
  • In this context, "expected" means average if the process is repeated many times
  • The "expected" return does not even have to be a possible return


$E(R)=\sum\limits_{i=1}^Np_iR_i$

Example: E(R)

Suppose you have predicted the following returns for stocks C and T in three possible states of the economy. What are the expected returns?
State Probability C T
Boom 0.3 0.15 0.25
Normal 0.5 0.1 0.2
Recession ??? 0.02 0.01
Expected Return 9.9% 17.7%
What is the risk premium if the US treasury bill rate is 4.15%? C=5.75%  T=13.55%

Variance and Standard Deviation

  • Variance and standard deviation measure the volatility of returns
  • Using unequal probabilities for the entire range of possibilities
  • Weighted average of squared deviations


$\sigma^2=\sum\limits_{i=1}^np_i(R-E(R))^2$

Example

State $P_i$ C T $p_i(R_C-E(R))^2$ $p_i(R_T-E(R))^2$
Boom 0.3 0.15 0.25 $0.3(0.15-0.099)^2$ $0.3(0.25-0.177)^2$
Normal 0.5 0.1 0.2 $0.5(0.1-0.099)^2$ $0.5(0.2-0.177)^2$
Recession 0.2 0.02 0.01 $0.2(0.02-0.099)^2$ $0.2(0.01-0.177)^2$
         $\sigma^2$ 0.002029 0.007441
         $\sigma$ 4.50% 8.63%

Portfolios

What is a portfolio?

  • A portfolio is a collection of assets
  • An asset's risk and return are important in how they affect the risk and return of the portfolio
  • The risk-return trade-off for a portfolio is measured by the portfolio expected return and standard deviation, just as with individual assets

Portfolio Weights

Suppose you have $\$$15,000 to invest and you have purchased securities in the following amounts. What are your portfolio weights in each security?
Portfolio Weights
$\$$2000 of DIS 2/15=13.33%
$\$$3000 of KO 3/15=20%
$\$$4000 of AAPL 4/15=26.7%
$\$$6000 of PG 6/15=40%

Portfolio Expected Return

The expected return of a portfolio is the weighted average of the expected returns of the respective assets in the portfolio

$E(R_p)=\sum\limits_{j=1}^mw_jE(R_j)$

  • You can also find the expected return by finding the portfolio return in each possible state and computing the expected value as we did with individual securities

Example

Stock Weight Return $w_jE(R_j)$
DIS .1333 19.69% 2.62%
KO .20 5.25% 1.05%
AAPL .267 16.65% 4.45%
PG .40 18.24% 7.30%
$E(R_p)$ 15.41%

Portfolio Variance

  1. Compute the portfolio return for each state.
  2. Compute the expected portfolio return using the same formula as for an individual asset.
  3. Compute the portfolio variance and standard deviation using the same formulas as for an individual asset.

Example

State $P_i$ A (50%) B (50%) $E(R_{p,i})$ $p_i(E(R_{p,i})-E(R_p))^2$
Boom .4 30% -5% 12.5% $.4(12.5-9.5)^2=3.6$
Bust .6 -10% 25% 7.5% $.6(7.5-9.5)^2=2.4$
$E(R_j)$ 6% 13% $E(R_p)$9.5%           $\sigma_p^2$=6
$\sigma_j^2$ 384 216           $\sigma_p$=2.45%
$\sigma_j$ 19.6% 14.7%


Note: You CANNOT use stock level $\sigma^2$ and $\sigma$ to calculate portfolio.

Risk, Return, and Diversification

Systematic Risk

  • Risk factors that affect a large number of assets
  • Also known as non-diversifiable risk or market risk
  • Includes such things as changes in GDP, inflation, interest rates, etc.

Unsystematic Risk

  • Risk factors that affect a limited number of assets
  • Also known as unique risk and asset-specific risk
  • Includes such things as labor strikes, part shortages, etc.

Returns

$Total Return = Expected Return + Unexpected Return$

 $Unexpected Return = Systematic Portion $
$+ Unsystematic Portion$

 $Total Return= Expected Return + Systematic Portion$
$+ Unsystematic Portion$

Diversification

Portfolio diversification is the investment in several different asset classes or sectors
  • Diversification is not just holding a lot of assets
  • For example, if you own 50 Internet stocks, you are not diversified
  • However, if you own 50 stocks that span 20 different industries, then you are diversified

The Principle of Diversification

  • Diversification can substantially reduce the variability of returns without an equivalent reduction in expected returns
  • This reduction in risk arises because worse than expected returns from one asset are offset by better than expected returns from another
  • However, there is a minimum level of risk that cannot be diversified away and that is the systematic portion

Diversifiable vs Non-Diversifiable Risk

Uber

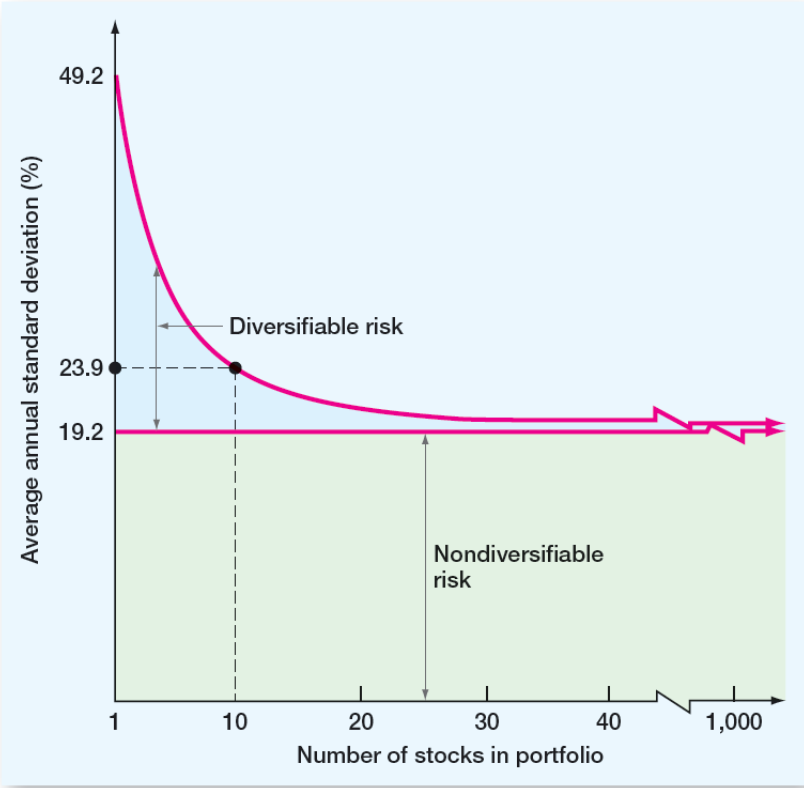
Diversifiable Risk

  • The risk that can be eliminated by combining assets into a portfolio
  • Often considered the same as unsystematic, unique or asset-specific risk
  • If we hold only one asset, or assets in the same industry, then we are exposing ourselves to risk that we could diversify away

Total Risk

Total risk = systematic risk + unsystematic risk

  • The standard deviation of returns is a measure of total risk
  • For well-diversified portfolios, unsystematic risk is very small
  • Consequently, the total risk for a diversified portfolio is essentially equivalent to the systematic risk

Systematic Risk Principle



There is a reward for bearing risk; There is not a reward for bearing risk unnecessarily. The expected return on a risky asset depends only on that asset's systematic risk since unsystematic risk can be diversified away.

Measuring Systematic Risk

  • How do we measure systematic risk?
    • We use the beta coefficient
  • What does beta tell us?
    • A beta of 1 implies the asset has the same systematic risk as the overall market
    • A beta < 1 implies the asset has less systematic risk than the overall market
    • A beta > 1 implies the asset has more systematic risk than the overall market

Current Beta's


Uber

Total vs. Systematic Risk

Consider the following information:
Standard Deviation Beta
Marathon Oil 20% 3.13
Exxon Mobil 30% 0.69


  • Which security has more total risk? Exxon Mobil
  • Which security has more systematic risk? Marathon Oil
  • Which security should have the higher expected return? Marathon Oil

Portfolio Beta

Consider the previous example with the following four securities
Security Weight Beta
DIS .133 1.444
KO .2 0.797
AAPl .267 1.472
PG .4 0.647

What is the portfolio beta?

.133(1.444) + .2(0.797) + .267(1.472) + .4(0.647) = 1.003

Portfolio Expected Returns and Betas

Uber

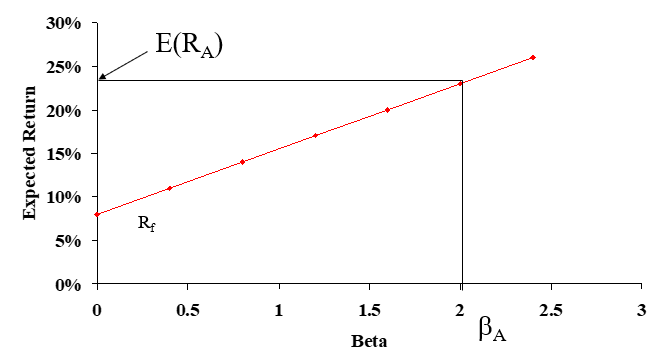
Reward-to-Risk Ratio

  • The reward-to-risk ratio is the slope of the line illustrated in the previous example

    • $Slope=\frac{E(R_A)-R_f}{\beta_A-0}$

    • From graph, $Slope=\frac{23-8}{2-0}=7.5$
  • What if an asset has a reward-to-risk ratio of 8 (implying that the asset plots above the line)?
  • What if an asset has a reward-to-risk ratio of 7 (implying that the asset plots below the line)?

Market Equilibrium

In equilibrium, all assets and portfolios must have the same reward-to-risk ratio, and they all must equal the reward-to-risk ratio for the market

$\frac{E(R_A)-R_f}{\beta_A}=\frac{E(R_M)-R_f}{\beta_M}$

Security Market Line

  • The security market line (SML) is the representation of market equilibrium
  • The slope of the SML is the reward-to-risk ratio: $\frac{E(R_M)-R_f}{\beta_M}$
  • But since the beta for the market is always equal to one, the slope can be rewritten
  • Slope $=E(R_M) – R_f =$ market risk premium

Put it all together...

Uber

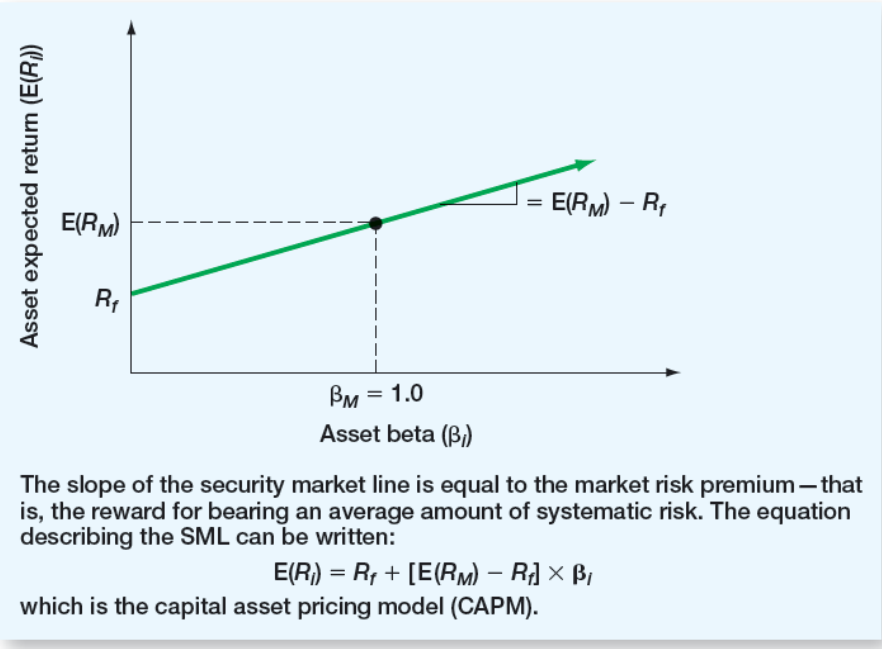
The Capital Asset Pricing Model (CAPM)

The capital asset pricing model defines the relationship between risk and return

$E(R_i)=R_f+\beta_i(E(R_M)-R_f)$

  • If we know an asset's systematic risk, we can use the CAPM to determine its expected return
  • This is true whether we are talking about financial assets or physical assets

Factors Affecting Expected Return

  1. Pure time value of money: measured by the risk-free rate
  2. Reward for bearing systematic risk: measured by the market risk premium
  3. Amount of systematic risk: measured by beta

CAPM: Example

Consider the betas for each of the assets given earlier. If the risk-free rate is 4.15% and the market risk premium is 8.5%, what is the expected return for each?
Asset Beta $E(R_i)$
DIS 1.444 4.15 + 1.444(8.5) = 16.42%
KO 0.797 4.15 + 0.797(8.5) = 10.92%
AAPL 1.472 4.15 + 1.472(8.5) = 16.66%
PG 0.647 4.15 + 0.647(8.5) = 9.65%

Extra Practice

Example 1

One year ago, Avril purchased 3,600 shares of Lavigne stock for $\$$101,124. Today, she sold those shares for $\$$26.60 a share. What is the total return on this investment if the dividend yield is 1.7 percent?

Example 2

A stock has yielded returns of 6 percent, 11 percent, 14 percent, and -2 percent over the past 4 years, respectively. What is the standard deviation of these returns? 

Example 3

You purchased 1,300 shares of LKL stock 5 years ago and have earned annual returns of 7.1 percent, 11.2 percent, 3.6 percent, -4.7 percent and 11.8 percent. What is your arithmetic average return?What is the geometric return?

Example 4

What is the expected return, variance, and standard deviation?
State Probability Go Nuts for Donuts Inc.
Boom .25 .15
Normal .5 .08
Slowdown .15 .04
Recession .10 -.03

Example 5

Consider the following information on returns and probabilities:

State Probability Apple Disney
Boom .25 15% 10%
Normal .6 10% 9%
Recession .15 5% 10%


What are the expected return and standard deviation for a portfolio with an investment of $\$$6,000 in Apple and $\$$4,000 in Disney?

Example 6

The risk free rate is 4%, and the required return on the market is 12%.
  1. What is the required return on an asset with a beta of 1.5?
  2. What is the reward/risk ratio?
  3. What is the required return on a portfolio consisting of 40% of the asset above and the rest in an asset with an average amount of systematic risk?

Why Cost of Capital is Important?

  • We know that the return earned on assets depends on the risk of those assets
  • The return to an investor is the same as the cost to the company
  • Our cost of capital provides us with an indication of how the market views the risk of our assets
  • Knowing our cost of capital can also help us determine our required return for capital budgeting projects

Required Return

  • The required return is the same as the appropriate discount rate and is based on the risk of the cash flows
  • We need to know the required return for an investment before we can compute the NPV and make a decision about whether or not to take the investment
  • We need to earn at least the required return to compensate our investors for the financing they have provided

Financial Policy and Cost of Capital

Big picture

  • A firm's cost of capital reflects the required return on the firm's assets as a whole
  • A firm uses both debt and equity capital
  • Cost of capital will be a mixture

Cost of Equity

  • The cost of equity is the return required by equity investors given the risk of the cash flows from the firm
  • There are two major methods for determining the cost of equity
    • Dividend Growth Model
    • SML, or CAPM

DGM Approach: Reminder



$R_E=\frac{D_1}{P_0}+g$

DGM: Pros and Cons

  • Advantages
    • easy to understand and use
  • Disadvantages
    • Requires a dividend payment
    • Requires growth rate to be constant
    • Extremely sensitive to growth rate estimate
    • Does not explicitly consider risk

SML Approach: Reminder



$R_E=R_f+\beta_E(E(R_M)-R_f)$

SML or CAPM: Pros and Cons

  • Advantages
    • Explicitly adjusts for systematic risk
    • Applicable to all companies, as long as we can estimate beta
  • Disadvantages
    • Have to estimate the expected market risk premium, which does vary over time
    • Have to estimate beta, which also varies over time
    • We are using the past to predict the future, which is not always reliable

Cost of Debt

  • The cost of debt is the required return on our company's debt
  • We usually focus on the cost of long-term debt or bonds
  • The required return is best estimated by computing the yield-to-maturity on the existing debt
  • The cost of debt is NOT the coupon rate

Weighted Average Cost of Capital (WACC)

  • We can use the individual costs of capital that we have computed to get our "average" cost of capital for the firm
  • This "average" is the required return on the firm's assets, based on the market's perception of the risk of those assets
  • The weights are determined by how much of each type of financing is used

Capital Structure Weights

  • Notation
    • E = market value of equity = # of outstanding shares times price per share
    • D = market value of debt = # of outstanding bonds times bond price
    • V = market value of the firm = D + E
  • Weights
    • $w_E = \frac{E}{V} =$ percent financed with equity
    • $w_D=\frac{D}{V}=$ percent financed with debt

Taxes

  • We are concerned with after-tax cash flows, so we also need to consider the effect of taxes on the various costs of capital
  • Interest expense reduces our tax liability
    • This reduction in taxes reduces our cost of debt
  • Dividends are not tax deductible, so there is no tax impact on the cost of equity

WACC



$WACC=w_ER_E+w_DR_D(1-T_C)$

Large Example

Go Nuts for Donuts! Inc.

Go Nuts for Donuts! Inc. has 50,000,000 shares outstanding that currently trade at $\$$80 a share. The firm recently paid a dividend of $\$$3.5 and its past 5-year growth rate in dividends is 6%. It's systematic risk, measured by beta, is 1.15. The firm has $\$$1 billion in outstanding debt, face value. The current quote on the bond is 110 and the coupon rate is 9% (semi-annual coupon payments). The bonds have 15 years to maturity. Assume a tax rate of 40%. The market risk premium is 9% and the risk free rate is 5%.

Solution: Cost of Equity


What is the Cost of Equity?

  • Dividend Growth Model
    • $R_E=\frac{D_1}{P_0}+g=\frac{3.5(1.06)}{80}+.06=.106375=10.64%$

  • CAPM
    • $R_E=R_f+\beta_E(E(R_M)-R_f)=5+1.15(9)=15.35%$

Solution: Cost of Debt


What is the Cost of Debt?

  • N=15*2=30
  • I%=3.927*2=$7.854=R_D$
  • PV=-1100
  • PMT=90/2=45
  • FV=1000


What is the After-Tax Cost of Debt?
 $R_D(1-T_C)=7.854(1-.4)=4.712%$

Solution: Weights


What are the capital structure weights?

  • E=50,000,000*80= 4 billion
  • D=1,000,000,000*1.1=1.1 billion
  • V=4 + 1.1 = 5.1 billion
  • $w_E=\frac{E}{V}=\frac{4}{5.1}=.7843$
  • $w_D=\frac{D}{V}=\frac{1.1}{5.1}=.2157$

Solution


What is the WACC?

  • Using DGM:
    • $WACC=w_ER_E+w_DR_D(1-T_C)$
    $WACC=.7843(10.64)+.2157*(7.854(1-.4)=9.36$
  • Using CAPM:
    • $WACC=w_ER_E+w_DR_D(1-T_C)$
    $WACC=.7843(15.35)+.2157*(7.854(1-.4)=13.06$

Issues with WACC

SML and WACC

Uber

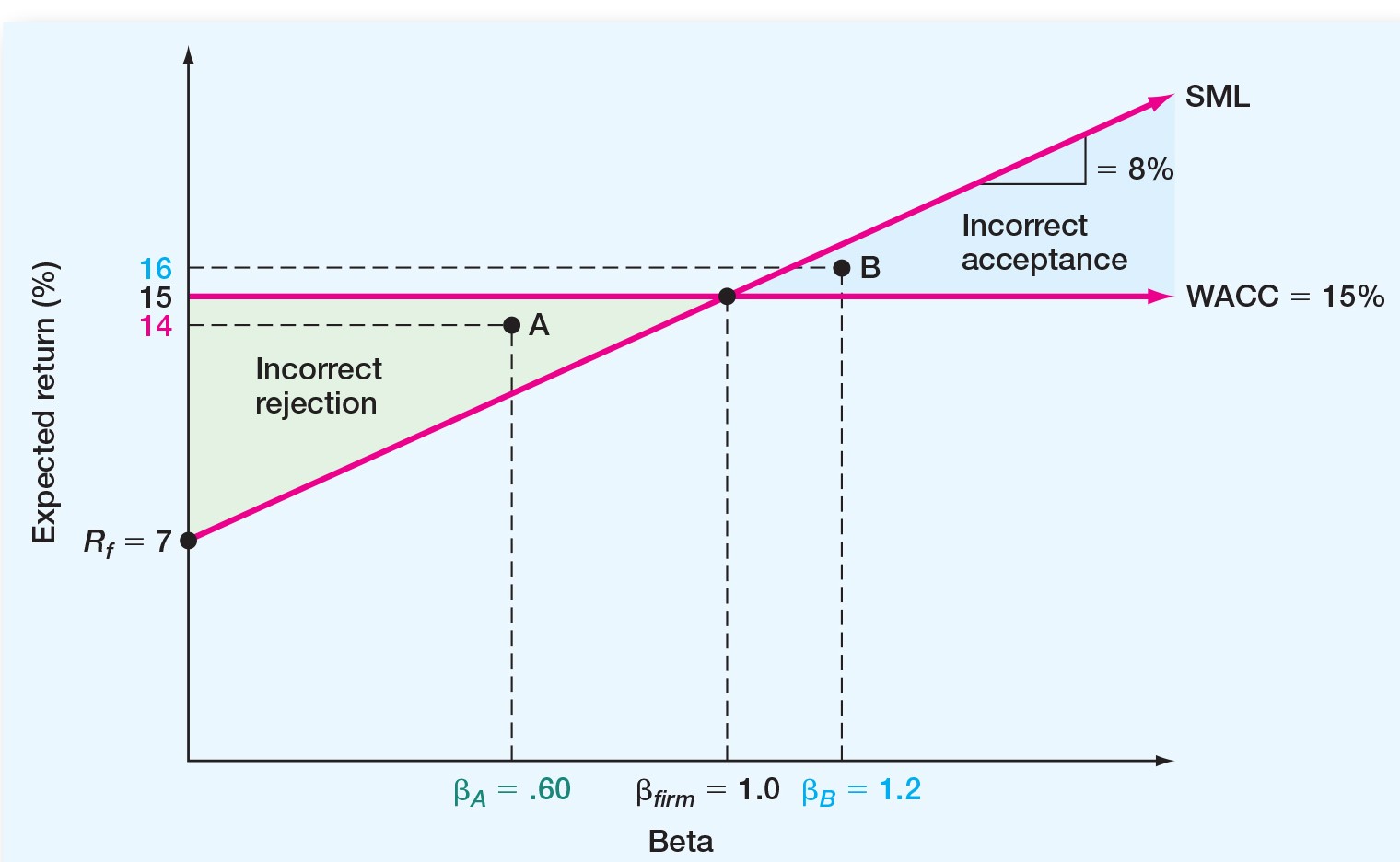
Divisions and WACC

WACC is only appropriate if the project has the same risk as the firm
  • Using firm-level WACC can lead to:
    • Incorrectly accepting high risk projects if $\beta$ of project is higher
    • Incorrectly rejecting low risk projects if $\beta$ of project is lower
  • Solutions:
    1. Pure Play: Use similar investment(company) in marketplace
    2. Subjective: Make risk adjustments to WACC.

Extra Practice

Example 1

  1. Suppose your company has an equity beta of .58, and the current risk-free rate is 6.1%. If the expected market risk premium is 8.6%, what is your cost of equity capital?
  2. Suppose that your company is expected to pay a dividend of $\$$1.50 per share next year. There has been a steady growth in dividends of 5.1% per year and the market expects that to continue. The current price is $\$$25. What is the cost of equity?
  3. Suppose we have a bond issue currently outstanding that has 25 years left to maturity. The coupon rate is 9%, and coupons are paid semiannually. The bond is currently selling for $\$$908.72 per $\$$1,000 bond. What is the cost of debt?

Example 2

Suppose you have a market value of equity equal to $\$$500 million and a market value of debt equal to $475 million. What are the capital structure weights?

Example 3

A corporation has 10,000 bonds outstanding with a 6% annual coupon rate, 8 years to maturity, a $\$$1,000 face value, and a $\$$1,100 market price. The company's 500,000 shares of common stock sell for $\$$25 per share and have a beta of 1.5. The risk free rate is 4%, and the market return is 12%. Assuming a 40% tax rate, what is the company’s WACC?

Key Learning Outcomes

  • First Lesson: Average Returns
    • Historical returns
    • Risk Premium
  • Second Lesson: Return Variability
    • Standard deviation
  • Arithmetic vs Geometric return
  • Capital market efficiency
    • Efficient market hypothesis

Key Learning Outcomes

  • Calculate:
    • Expected return, variance, and standard deviation
    • Do so for a portfolio of assets
  • Understand diversification
    • Total risk, Systematic risk, Unsystematic risk
  • Beta, Security Market Line and CAPM
    • Understand concept and derivation
    • Calculate Portfolio Beta
    • Use CAPM

Notes on Notations

$R$= Return
$R_i$= Return for stock i (index (i) can be i, j, or any letter)
$\sigma^2_i$ Variance for stock i
$\sigma_i$ Standard deviation for stock i
$E(R_i)$= Expected return for stock i
$E(R_p)$= Expected return for a portfolio
$p_i$= Probability of state i occurring
$E(R_{p,i})$= Expected return of the portfolio in state i
$R_f$= risk free rate or expected return on the risk free asset
$\beta_i$= Beta of stock i    $\beta_m$= Beta of the market (equal to one)